Tìm m để hàm số nghịch biến trên khoảng (2 3) là để hàm số nghịch biến trên khoảng (2, 3), chúng ta cần điều kiện là đạo hàm của hàm số phải âm trên khoảng đó.
Giả sử hàm số được ký hiệu là f(x). Để tìm m, chúng ta cần kiểm tra dấu của đạo hàm f'(x) trên khoảng (2, 3).
Bước 1: Tính đạo hàm của hàm số f(x).
Bước 2: Đặt f'(x) < 0 và giải phương trình này để tìm các điểm x thỏa mãn.
Bước 3: Kiểm tra dấu của f”(x) tại các điểm x thỏa mãn f'(x) < 0. Nếu f”(x) > 0 tại các điểm đó, thì f(x) là hàm số nghịch biến trên khoảng (2, 3).
Tìm m để hàm số nghịch biến trên khoảng (2 3) gồm có lý thuyết về đồng biến và nghịch biến của hàm số, tìm m để hàm số đồng biến hay nghịch biến. Cùng hamhochoi.net tìm hiểu rõ hơn qua bài viết dưới đây.
Lý thuyết
Định nghĩa sự đồng biến, nghịch biến của hàm số.
Cho hàm số y = f(x) xác định trên K , trong đó K là một khoảng, đoạn hoặc nữa khoảng.
- Hàm số y = f(x) đồng biến trên nếu mọi x₁, x₂ ∊ K, x₁ < x₂ ⇒ f(x₁) < f(x₂).
- Hàm số y = f(x) nghịch biến trên K nếu mọi x₁, x₂ ∊ K, x₁ < x₂ ⇒ f(x₁) > f(x₂).
Mối quan hệ giữa tính đơn điệu(đồng biến,nghịch biến) của hàm số và dấu của đạo hàm.
- Nếu f'(x)≥0,∀x∈K thì fx đồng biến trên K.
- Nếu f'(x)≤0,∀x∈K thì fx nghịch biến trên K.
Một số điều kiện cần và đủ để hàm số đơn điệu
Điều kiện cần để hàm số đơn điệu:
Điều kiện cần để hàm số đơn điệu trên một khoảng là đạo hàm của hàm số không đổi dấu trên khoảng đó.
Cụ thể, nếu f(x) là một hàm số đơn điệu trên khoảng (a, b), thì điều kiện cần là f'(x) không đổi dấu trên khoảng đó. Nếu f'(x) ≥ 0 hoặc f'(x) ≤ 0 với mọi x trong khoảng (a, b), thì hàm số f(x) tương ứng là đơn điệu tăng hoặc giảm trên khoảng đó.
Điều kiện này chỉ là điều kiện cần và không đủ để hàm số đơn điệu. Để xác định tính đơn điệu của một hàm số, ta cần xem xét thêm các điểm uốn, điểm cực trị, và các khoảng ngoại lệ khác của hàm số.
Điều kiện đủ để hàm số đơn điệu:
- Điều kiện đơn điệu tuyến tính: Nếu đạo hàm của hàm số f(x) là một hằng số không âm hoặc không dương trên một khoảng xác định, thì hàm số f(x) là đơn điệu trên khoảng đó. Nếu đạo hàm là một hằng số không âm, hàm số là đơn điệu tăng; nếu đạo hàm là một hằng số không dương, hàm số là đơn điệu giảm.
- Điều kiện dựa trên đạo hàm: Nếu đạo hàm của hàm số f(x) không đổi dấu trên một khoảng xác định và không bằng 0 trên khoảng đó, thì hàm số f(x) là đơn điệu trên khoảng đó. Nếu đạo hàm luôn không âm (f'(x) ≥ 0) hoặc luôn không dương (f'(x) ≤ 0) trên khoảng, thì hàm số là đơn điệu tăng hoặc giảm tương ứng.
Điều kiện cần và đủ để hàm số đơn điệu là khi đạo hàm không đổi dấu trên khoảng và không bằng 0 trên khoảng đó.
Định lí đồng biến, nghịch biến và không đổi
- Nếu f'(x) > 0 với mọi x thuộc khoảng K, thì hàm số f(x) đồng biến trên khoảng K. Điều này có nghĩa là giá trị của hàm số tăng khi x tăng trên khoảng K.
- Nếu f'(x) < 0 với mọi x thuộc khoảng K, thì hàm số f(x) nghịch biến trên khoảng K. Điều này có nghĩa là giá trị của hàm số giảm khi x tăng trên khoảng K.
- Nếu f'(x) = 0 với mọi x thuộc khoảng K, thì hàm số f(x) không đổi trên khoảng K. Điều này có nghĩa là giá trị của hàm số không thay đổi khi x thay đổi trên khoảng K.
Chú ý: Những nhận xét và điều kiện trong câu hỏi cũng áp dụng khi hàm số liên tục trên một đoạn và có đạo hàm dương (a, b) hoặc đạo hàm âm (a, b) trên đoạn đó.
Định lí mở rộng và được gọi là Định lí đồng biến, nghịch biến mở rộng.
- Nếu f'(x) ≥ 0 với mọi x thuộc khoảng K và f'(x) = 0 xảy ra tại một số hữu hạn điểm của K, thì hàm số f(x) đồng biến trên khoảng K. Điều này có nghĩa là giá trị của hàm số tăng hoặc không giảm khi x tăng trên khoảng K, và sự không giảm này xảy ra tại các điểm xứng với f'(x) = 0.
- Nếu f'(x) ≤ 0 với mọi x thuộc khoảng K và f'(x) = 0 xảy ra tại một số hữu hạn điểm của K, thì hàm số f(x) nghịch biến trên khoảng K. Điều này có nghĩa là giá trị của hàm số giảm hoặc không tăng khi x tăng trên khoảng K, và sự không tăng này xảy ra tại các điểm xứng với f'(x) = 0.
Định lí mở rộng này cho phép có sự tồn tại của các điểm tắt đạo hàm (f'(x) = 0) trên khoảng K, và vẫn có thể kết luận tính đơn điệu của hàm số trên khoảng đó dựa trên dấu của f'(x) trước và sau các điểm tắt đạo hàm.
Quy tắc xét tính đơn điệu của hàm số
Bước 1: Tìm tập xác định D của hàm số f(x).
Bước 2: Tính đạo hàm f'(x) của hàm số f(x). Xác định các điểm x_i (i = 1, 2, …, n) mà tại đó f'(x_i) = 0 hoặc f'(x_i) không xác định.
Bước 3: Sắp xếp các điểm x_i theo thứ tự tăng dần và lập bảng biến thiên của hàm số. Trong bảng biến thiên, ta sẽ chia khoảng giữa các điểm x_i thành các khoảng con và xác định tính chất đồng biến, nghịch biến trên từng khoảng con đó.
Bước 4: Dựa vào bảng biến thiên, ta rút ra kết luận về tính đơn điệu của hàm số f(x) trên các khoảng con. Cụ thể, ta xác định được các khoảng đồng biến và nghịch biến của hàm số f(x).
Lưu ý: Trong trường hợp hàm số f(x) không xác định đạo hàm f'(x) tại một số điểm, ta cần xem xét các giá trị đặc biệt của hàm số để xác định tính chất đơn điệu tại những điểm đó.
Qua qui tắc xét tính đơn điệu, ta có thể xác định được các khoảng đồng biến và nghịch biến của hàm số, từ đó hiểu rõ hơn về sự biến thiên của hàm số trên tập xác định của nó.
Xem thêm bài viết:
Diện tích tam giác lớn nhất khi nào?
Phương trình hoành độ giao điểm là gì?
Tìm m để hàm số nghịch biến trên khoảng (2 3)
Để hàm số nghịch biến trên khoảng (2, 3), chúng ta cần điều kiện là đạo hàm của hàm số phải âm trên khoảng đó.
Giả sử hàm số được ký hiệu là f(x). Để tìm m, chúng ta cần kiểm tra dấu của đạo hàm f'(x) trên khoảng (2, 3).
Bước 1: Tính đạo hàm của hàm số f(x).
Bước 2: Đặt f'(x) < 0 và giải phương trình này để tìm các điểm x thỏa mãn.
Bước 3: Kiểm tra dấu của f”(x) tại các điểm x thỏa mãn f'(x) < 0. Nếu f”(x) > 0 tại các điểm đó, thì f(x) là hàm số nghịch biến trên khoảng (2, 3).
Tìm m để hàm số đồng biến, nghịch biến trên khoảng K là ℝ=-∞;+∞.
Phương pháp giải:
Bước 1: Tính y’. Hàm số được xem là đồng biến nếu y’ ≥ 0 và nghịch biến nếu y’ ≤ 0 với mọi x ∈ ℝ.
Bước 2: Thường gặp y’ là một tam thức bậc hai nên ta dựa vào các nhận xét sau để tìm m :
+ Bất phương trình ax2+bx+c≥0,∀x∈ℝ⇔a>0△≤0.
+ Bất phương trình ax2+bx+c≤0,∀x∈ℝ⇔a<0△≤0.
Ví dụ minh họa:
Ví dụ 1: Tìm m để hàm số y=-x3+m-3×2-m+3x+2020 nghịch biến trên -∞;+∞, ta cần tìm giá trị của m thỏa mãn y’ ≤ 0 với mọi x ∈ ℝ.
Cách giải:
- Ta có y’=-3×2+2m-3×2-m-3.
- Hàm số đồng biến trên -∞;+∞ khi:
y’≤0,∀x∈ℝ⇔-3×2+2m-3x-m-3≤0,∀x∈ℝ
⇔a=-1<0 (luôn đúng)△’=m-32-3-m-3≤0⇔m2-6m+9-3m-9≤0
⇔m2-9m≤0⇔0≤m≤9.
Ví dụ 2: Tìm m để hàm số y=13×3-2×2+m-2020x+3 đồng biến trên ℝ.
Cách giải:
- Ta có y’=x2-4x+m-2020
- Hàm số đồng biến trên ℝ khi :y’≥0,∀x∈ℝ⇔x2-4x+m-2020≥0,∀x∈ℝ⇔a=1>0 (luôn đúng)△’=22-1m-2020≤0⇔22-1m-2020≤0⇔m≥2024.
Tìm m để hàm số đồng biến, nghịch biến trên khoảng K là tập con của ℝ.
Phương pháp “Cô lập tham số m”
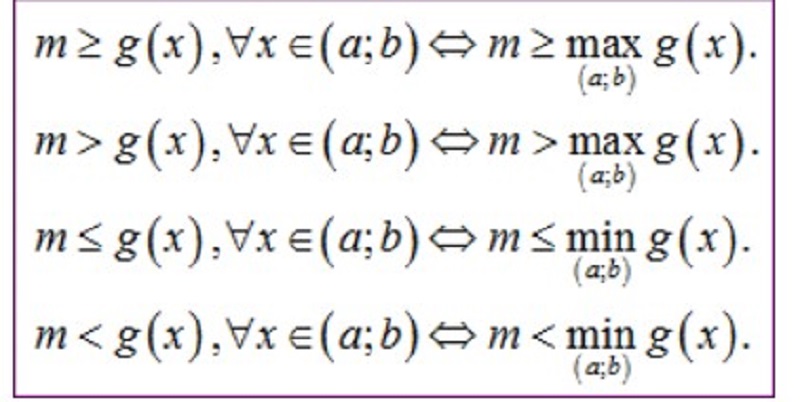
Cách giải:
Cho hàm số y=fx có đạo hàm trên K.
- Bước 1. Tính y’. Hàm số đồng biến(nghịch biến) trên K thì y’≥0,∀x∈K (y’≤0,∀x∈K).
- Bước 2. Đưa bất phương trình y’≥0,∀x∈K(y’≥0,∀x∈K) về dạng m≥g(x),∀x∈K hoặc m≤g(x),∀x∈K (ta gọi đây là bước cô lập m)
- Bước 3. Tìm m dựa vào hai nhận xét sau :
- m≥g(x),∀x∈K⇔m≥maxKg(x).
- m≤g(x),∀x∈K⇔m≤minKg(x).
Ví dụ: Tìm tất cả các giá trị của tham số m để hàm số fx=2×3+3×2-6mx-1 nghịch biến trên 0;2.
Cách giải;
- f’x=6×2+6x-6m.
- Để hàm số nghịch biến trên khoảng 0;2 ta có f’x≤0,∀x∈0;2⇔6×2+6x-6m≤0,∀x∈0;2⇔x2+x-m≤0,∀x∈0;2⇔m≥x2+x=gx,∀x∈0;2⇔m≥max0;2gx.
- Xét gx=x2+x⇒g’x=2x+1>0,∀x∈0;2 hay hàm số đồng biến trên 0;2, do đó : m≥max0;2gx=g2=6.
Phương pháp sử dụng bảng biến thiên giải dạng toán tìm m để hàm số đồng biến (nghịch biến) trên một khoảng:

Phương pháp “Cô lập tham số m” có thể tương đối dài dòng và phức tạp trong việc giải quyết một số bài toán. Tuy nhiên, nó là một phương pháp linh hoạt và mạnh mẽ, có thể áp dụng cho hầu hết các trường hợp.
Cách giải :
- Bước 1. Tính y’. Hàm số đồng biến(nghịch biến) trên K thì y’≥0,∀x∈K (y’≤0,∀x∈K).
- Bước 2. Lập bảng biến thiên của hàm số dựa vào dấu y’.
- Bước 3. Từ bảng biến thiên và đề bài kết luận giá trị của m.
Chú ý :
- Nếu dấu của đạo hàm phụ thuộc vào dấu của một tam thức bậc hai thì ta phải xét hai trường hợp △≤0 và △>0.
- Khi sử dụng phương pháp này ta thường dẫn đến việc so sánh các nghiệm của một tam thức bậc hai với một số α liên quan. Khi đó ta có thể đưa bài toán học đến việc vận dụng định lý Vi-et bằng cách sử dụng các kết quả sau :
- x1<α<x2⇔x1-αx2-α<0⇔x1x2-αx1+x2+α2<0.
- x1<x2<α⇔x1-αx2-α>0x1+x22-α<0.
- α<x1<x2⇔x1-αx2-α>0x1+x22-α>0
Ví dụ: Tìm m để hàm số y=13×3+(m-1)x2+(m2-3m+2)x+4 đồng biến trên 2;+∞.
Cách giải :
Ta có y’=x2+2(m-1)x+(m2-3m+2)
Hàm số đồng biến trên 2;+∞ khi y’=x2+2(m-1)x+(m2-3m+2)≥0,∀x∈2;+∞.
Cách 1 :
- Nếu △’≤0⇔m-12-m2-3m+2≤0⇔m-1≤0⇔m≤1 thì y’≥0,∀x∈ℝ. Do đó hàm số đồng biến trên ℝ nên cũng đồng biến trên 2;+∞.
- Vậy m≤1 thỏa yêu cầu bài toán (1)
Cách 2 :
- Nếu △’>0⇔m>1 thì y’ có hai nghiệm phân biệt x1<x2. Ta có bảng biến thiên như sau:
-
-
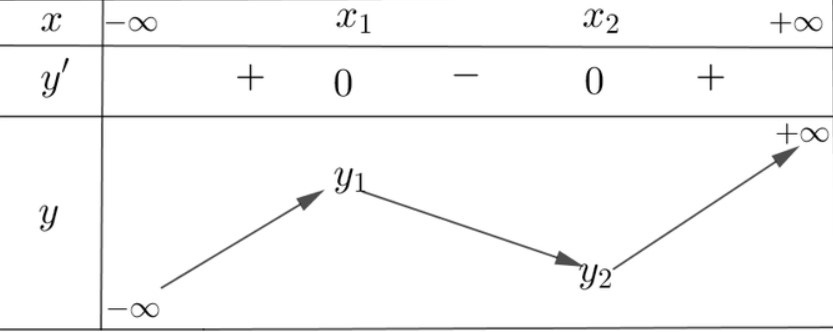
Bảng biến thiên
-
- Dựa vào bảng biến thiên để hàm số đồng biến trên 2;+∞ thì 2;+∞⊂x2;+∞, có nghĩa là y’=x2-2(m-1)x+(m2-3m+2)=0 có hai nghiệm thỏa x1<x2≤2⇔x1-2×2-2≥0x1+x22-2<0⇔x1x2-2×1+x2+4≥0x1+x2-4<0⇔m2-3m+2-2(2m-2)+4≥02m-2-4<0⇔m2-7m+10≥02m<6⇔m≤2 hoặc m≥5m<3⇔m≤2.
- Kết hợp với điều kiện m>1 ta có 1<m≤2 (2)
Hy vọng với bài viết tìm m để hàm số nghịch biến trên khoảng ( 2 3 ) ở trên sẽ giúp ích cho các bạn. Mọi thắc mắc và góp ý các bạn hãy để lại bình luận dưới bài viết để hamhochoi ghi nhận và hỗ trợ. Chúc các bạn thành công.
